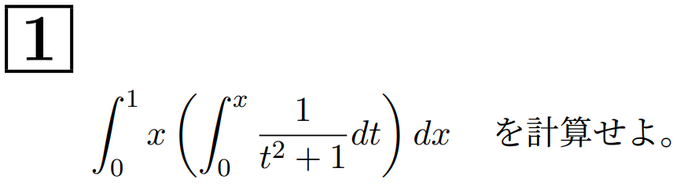【1日目】定積分で表された関数と逆関数の積分【1日1問つくる会】
少し癖がある実戦的な問題をXで毎日更新している1日1問。
「積分区間に変数xを含むときの対処法」「隠された逆関数」という視点から2つの解法を紹介します。
過去の記事とも関連があるのでそちらも紹介します。
問題
解答


解説
【解答1】では、定積分で表された関数 は積分区間に変数
が入っていることから微分すると被積分関数が出てくる、いわゆる微分積分学の基本定理を活かすために部分積分をしようという考え方をとりました。
最終的に という具体的な値を計算するために置換積分も用いています。
【解答2】では の正体を探っています。
結果的に解答にも書いているように は
の逆関数であることが分かります。
その後は逆関数であることを活かすために置換積分を用いています。
しかし結果的にではありますが最後は部分積分を使っています。
【解答1】と【解答2】には違いもありますが、共通点もあります。
実はそのような記事を過去に書いていました。
手前味噌ですがぜひそちらもご参照ください。
「1日1問つくる会」とは?
2024年末に思い立って2025年に入ってから1日1問ずつ問題をXで公開しています。
終了条件は「投稿が途絶えた場合」です。
今のところ30問以上は続いていますので、随時本サイトで解答解説を公開していきます!
【2025年1日1問つくる会】
— ふくま数学🐙 (@Fukuma_topology) 2024年12月31日
スレッドに大学入試レベルの数学の問題を1日1問投稿します!
投稿が途絶えるまで毎日投稿します(最悪の場合1日で終了します)
解答は気が向いたら何かしらどこかしらで発信する予定ですが、ぜひリプライ、引用などで言っちゃってください!#1日1問つくる会 pic.twitter.com/ENGMn5N4Fx