とぽろじい　～大人の数学自由研究～

高校数学から分かる新しい数学、大学で学ぶ数学を少しずつまとめていくブログです。ゆくゆくは本にまとめたいと思っています。

【組合せ論】メビウスの反転公式1　「導入：整数だけじゃない、メビウスの反転公式で高校数学を俯瞰する」

★大学数学 *【組合せ論】メビウスの反転公式・組合せ論

このシリーズでは高校数学でも話題となることがある(古典的な)メビウスの反転公式について、より一般化された形で導入し、高校数学に出てくる複数の公式を包括的・横断的に証明しようという目論見のもと書いていこうと思います。

↓YouTubeで概要を動画にまとめました(2023.5.26)

math-topology.hatenablog.com

【本シリーズのレベル】

大学数学

【本シリーズに対する予備知識】

高校数学(現行教育課程のⅠAⅡBまで)

集合と位相(冪集合が分かる程度。なくてもいけるかも。)

群論・環論(知っていると納得しやすいが必須ではないです)

【参考文献】(随時追加予定)

[Sta] Richard P. Stanley, Enumerative Combinatorics, Cambridge University Press40 W. 20 St. New York, NYUnited States, 2012.

リンク

さて、そもそも古典的なメビウスの反転公式とはどのようなものなのでしょうか。

今回の導入で触れておきましょう。

古典的なメビウスの反転公式

$1$ 以上の自然数の集合 $\mathbb{Z}_{\ge 1}$ 上で定義され、複素数を値にもつメビウス関数 $\mu$ つまり写像

$\mu : \mathbb{Z}_{\ge 1} \longrightarrow \mathbb{C}$

を以下で定義します。

$1$ 以上の自然数 $n$ について

$\mu (n)= \left\{ \begin{array}{} 0　　　　(ある素数 p について p^{2}で割り切れる)\\ 1　　　　(n=1) \\(-1)^{k} 　　(n\neq 1, 相異なる k 個の素因数をもつ)\end{array} \right.$

さて、2つの写像

$f : \mathbb{Z}_{\ge 1} \longrightarrow \mathbb{C}$

$g : \mathbb{Z}_{\ge 1} \longrightarrow \mathbb{C}$

について考えます。

このとき以下の公式が成り立ちます。

公式(古典的なメビウスの反転公式)

$f$ と $g$ が

$g(n)=\displaystyle \sum_{d|n} f(d)$

を満たすとき，

$f(n)=\displaystyle \sum_{d|n} \mu(d)g(\frac{n}{d})=\sum_{d|n} \mu(\frac{n}{d})g(d)$

が成り立つ。*1

( $\displaystyle \sum_{d|n}$ は $n$ のすべての正の約数 $d$ についてわたる和を表します。)

この公式を古典的なメビウスの反転公式(Classical Möbius inversion formula)と呼びます。

しかし、これだけではどのようなものかがイメージできません。

具体例(約数の個数)

$f(n)=1$ で定まる定数関数 $f$ と、

$g(n)=(\,n\, の正の約数の個数)$ で定まる関数 $g$ を考えます。

このとき

$g(n)=\displaystyle \sum_{d|n} f(d)$

を満たすので、メビウスの反転公式を用いることで

$f(n)=\displaystyle \sum_{d|n} \mu(d)g(\frac{n}{d})$

が成り立ちます。

たとえば $n=12$ のときは、

$1=\mu(1)g(12)+\mu(2)g(6)+\mu(3)g(4)+\mu(4)g(3)+\mu(6)g(2)+\mu(12)g(1)$

となることと、 $\mu$ の定義から

$1=g(12)-g(6)+g(4)+g(2)$

となります。

このことは関数 $f$ の和で表される関数 $g$ について、 $g$ のある種の交代和により $f$ が再現されることを意味しています。

また、この例に注目すると $n$ の正の約数の個数は、「 $n$ の正の約数たち」の正の約数の個数の足し引きで表されることになります。*2

関連事項や証明について

詳細は以下のWikipediaの記事やネットの記事をご参照ください。

(本シリーズでは、一般化した形での証明を与えます。)

ja.wikipedia.org

(畳み込みにより「反転」の"気持ち"が表現されています。)

mathtrain.j(こちらに簡明な証明が紹介されています)

Posetに一般化

本シリーズでは古典的なメビウスの反転公式は「あくまで一例」として扱いたいと考えています。

そこで本格的に定義や定理などを紹介する前に、「なぜ一般化できるのか」という部分を簡単に押さえておこうと思います。

古典的なメビウスの反転公式では

$\displaystyle\sum_{d|n}$

といったように、自然数の正の約数について足し合わせました。

この正の約数というものには1つの特徴があります。

それは一種の「良い向き」があるということです。

たとえば $3$ は $6$ の約数でかつ、 $6$ は $12$ の約数であるので、 $3$ は $12$ の約数でもあります。

しかし $6$ は $3$ の約数ではありません。

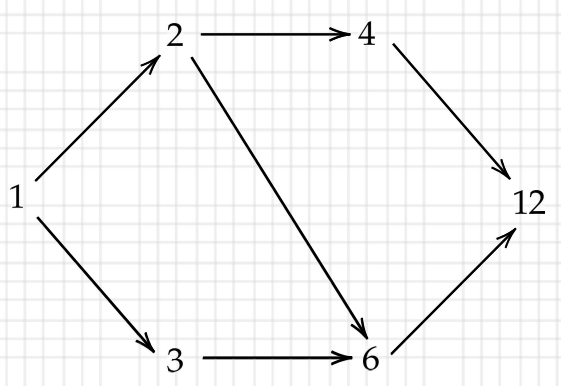
f:id:kfukui-math7:20201122233155p:plain — (上の図は「〇は◇の約数である」を〇→◇で表しています。)

このような性質をもつものは「約数」だけではありません。

実数の大小関係や集合の包含関係など、様々な場面で見られます。

これをPosetという用語を使って扱っていきます。

というわけで「メビウスの反転公式も様々な場面で定義できないか」というのが今回の1つのモチベーションになります。

まだまだ先が見えませんが、以下のことを、一般化されたメビウスの反転公式の結果の1つとして扱おうと思います。

古典的なメビウスの反転公式
差分と和分の関係(差分和分学の基本定理)
包除原理(inclusion-exclusion)
オイラーの多面体定理

どれも高校数学の話題としても出てくるものですね。

というわけで、今回の裏テーマは「大学数学の大道具を使って高校数学を俯瞰する」というものになります。

ややマニアックな話題になりますが、雰囲気だけでも知ってもらえたらうれしく思います。

math-topology.hatenablog.com

それでは今回はこのあたりにして、次回より本格的に定義や定理、その証明を展開していこうと思います。

それでは今回も最後までお読みいただき誠にありがとうございます。

次回もよろしくお願いします。

*1:逆も成り立ちます。

*2: $g(1)=1$ を左辺に適用すると $g(12)=g(1)-g(2)-g(4)+g(6)$ となります。

(C)2020-2022 ふくま All rights reserved.