
代数的トポロジー(Algebraic topology, 代数的位相幾何学)と言えば「ホモロジー群」「コホモロジー環」「ホモトピー群」 といったホモトピー不変量が登場します。
たとえばホモロジー群、コホモロジー環は『初見では定義が複雑な反面、簡単な計算法(切除同型、Mayor-Vietoris 完全列など)がある』一方、ホモトピー群は『定義が分かりやすい(球面からの基点付き写像のホモトピー類)反面、計算法は決して簡単ではない』という、"あちらを立てればこちらが立たず"の特徴があります。
今回は「LSカテゴリー( Lusternik-Schnirelmann category)」というホモトピー不変量を紹介するのですが、どちらかというとホモトピー群と同じように、「定義がかなり分かりやすい反面、計算は簡単ではない」タイプのホモトピー不変量になります。
では、「ホモトピー群との違いは何か?」ですが、それはLSカテゴリーは「0以上の自然数」という数値で与えられる点です。
ざっくり言うと「空間を"可縮な部分空間"で覆うには何枚必要か?」というものを考えることになります。
"可縮な部分空間"というのは"伸縮可能なハンカチ"のイメージですね。
さて、今回は証明などは少なめにLSカテゴリーの紹介を不定期に行っていこうと思います。
方向性はいろいろ考えられるゆえに未定です。
何かご要望等ございましたらぜひコメントや問い合わせフォームよりお願いします。
前提知識・参考文献とLSカテゴリーの定義
【本シリーズのレベル】
大学数学
【本シリーズに対する予備知識】(随時更新予定)
集合と位相(連続写像やコンパクトの意味や周辺知識を知っているくらいでも。)
代数的トポロジー(ホモトピー同値をなんとなく知っているくらいでも。)
【参考文献】(随時追加予定)
[CLOT] O. Cornea, G. Lupton, J. Oprea, and D. Tanr´e, Lusternik-Schnirelmann category,
vol. 103 of Mathematical Surveys and Monographs. American Mathematical Society, Providence, RI, 2003.
(日本では九州大の岩瀬先生が長年研究されており、先生のウェブサイトからもたくさんの情報が得られますのでお勧めです。)
(代数的トポロジーについては入門書がいろいろありますし、辞書的に引く場合には Allen Hatcher の website に電子版のテキストがあるので使えます。英語版 Wikipedia 等も情報は充実しています。あとは英語ですが、nLab も内容は充実していますね。)
それでは本題に入りましょう。
定義1(LSカテゴリー)
位相空間 について、
の有限開被覆
(
) で、各
に対して
が
において可縮、すなわち包含写像
が null-homotopic (定値写像とホモトピック) であるとき、
と定義する。
特に、このような整数 で最小であるものを
として
と書く。
(ただし、 はのとりうる値は0以上の整数もしくは
*1として定めます。)
具体例(ユークリッド空間と球面)
さっそく具体例を計算してみましょう。
(例1) 次元ユークリッド空間
普通の距離により決まる位相により は可縮ですから、
自体が自身の可縮な開被覆を与えます。
したがって となり、定義により、
となります。
(例2) 次元球面
次元ユークリッド空間
の部分空間
次元球面
について次の
,
が可縮な開被覆を与えます。
したがって となります。
一方で は可縮ではないので、
となります。
したがって前半の結果と合わせることで
を得ます。
ホモトピー不変量であることの証明
次にLSカテゴリーがホモトピー不変量であることを示しておきましょう。
(証明)
とします。
すると定義1から の有限開被覆
(
) で、各
に対して
が
において可縮なものが存在します。
このような開被覆を一つ取ります。
次に がホモトピー同値を与えるとし、ホモトピー逆写像を
とします。
において
(
)が可縮な開被覆を与えてくれるなら証明が終わります。
そこで各 について包含写像
を与えておきます。
定義1から は null-homotopic です。
すると次の写像も null-homotopic になります。
一方でこの写像は包含写像 ともホモトピックですから
は
において可縮です。
ゆえに となります。
逆に ならば
も成り立つのは明らかです。
以上より が得られます。
(証明終わり)
LSカテゴリーの壁
ここまでは非常に"順調"で、様々な対象のLSカテゴリーが計算できそうですね。
最後にトーラスに触れておきましょう。
(例3) トーラス
2次元ユークリッド空間 の部分空間としてトーラス
を考えましょう。
補題1により、LSカテゴリーはホモトピー不変量ということが分かったので、トーラスのどの表し方でもLSカテゴリーが一致することが保証されています。
そこで今回は可縮な開被覆を与えるために以下の正方形の貼り合わせを用いましょう。

(青矢印同士、赤矢印同士を向きを合わせて貼り付ける(同一視する)とトーラスが出来上がります。)
よって上の図形をもとに可縮な開被覆を構成すれば十分となります。
少しいびつですが…
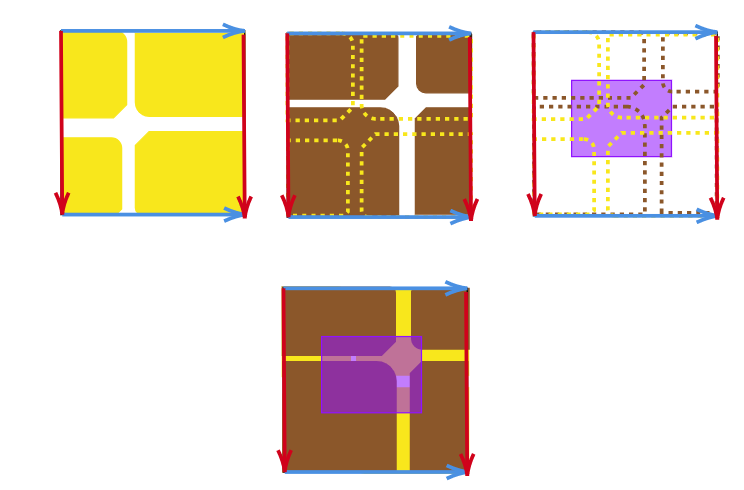
上のように「黄色」「茶色」「紫」の3つの開集合が可縮な開被覆を与えています。*2
したがって が言えます。
また、トーラスもまた可縮ではないので です。
したがって または
のいずれか一方であると絞り込めます。
ただ、残念ながら2枚の可縮な開集合によって開被覆を作ることは出来ません。
そして、具体的に開被覆を構成するのと「存在しない」では全く別の話になってしまいます。
そのためLSカテゴリーには下からの評価が必要不可欠となります。
また、今回は具体的な開被覆を構成しましたが、別のホモトピー不変量を用いて上からの評価ができればそれに越したことはありません。
LSカテゴリーは「不等式による評価」が一つのテーマつまり"壁"になりそうですね。
トーラスでさえ直接計算が難しいのでなかなか大変そうです。
まとめ
さて今回は1回目ということでここまでにします。
次回はLSカテゴリーを様々な代数的トポロジーの道具を用いて評価するという手法をご紹介する予定です。
それでは最後までお読みいただきありがとうございました。
次回もどうぞよろしくお願いします。